publications

2023

1. 

   The Complexity of Homomorphism Reconstructibility

   Jan Böker, Louis Härtel, Nina Runde, and 2 more authors

   2023

   Abs arXiv

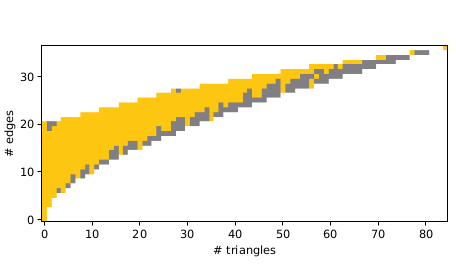
   Representing graphs by their homomorphism counts has led to the beautiful theory of homomorphism indistinguishability in recent years. Moreover, homomorphism counts have promising applications in database theory and machine learning, where one would like to answer queries or classify graphs solely based on the representation of a graph G as a finite vector of homomorphism counts from some fixed finite set of graphs to G. We study the computational complexity of the arguably most fundamental computational problem associated to these representations, the homomorphism reconstructability problem: given a finite sequence of graphs and a corresponding vector of natural numbers, decide whether there exists a graph G that realises the given vector as the homomorphism counts from the given graphs. We show that this problem yields a natural example of an \mathsfNP^#\mathsfP-hard problem, which still can be 𝖭𝖯-hard when restricted to a fixed number of input graphs of bounded treewidth and a fixed input vector of natural numbers, or alternatively, when restricted to a finite input set of graphs. We further show that, when restricted to a finite input set of graphs and given an upper bound on the order of the graph G as additional input, the problem cannot be 𝖭𝖯-hard unless 𝖯=𝖭𝖯. For this regime, we obtain partial positive results. We also investigate the problem’s parameterised complexity and provide fpt-algorithms for the case that a single graph is given and that multiple graphs of the same order with subgraph instead of homomorphism counts are given.

2. 

   The Parameterized Complexity of Learning Monadic Second-Order Logic

   Steffen Bergerem, Martin Grohe, and Nina Runde

   2023

   Abs arXiv

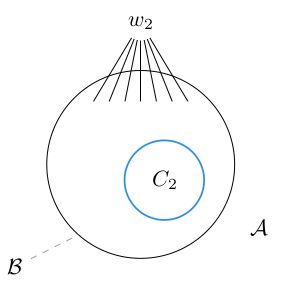
   Within the model-theoretic framework for supervised learning introduced by Grohe and Turán (TOCS 2004), we study the parameterized complexity of learning concepts definable in monadic second-order logic (MSO). We show that the problem of learning an MSO-definable concept from a training sequence of labeled examples is fixed-parameter tractable on graphs of bounded clique-width, and that it is hard for the parameterized complexity class para-NP on general graphs. It turns out that an important distinction to be made is between 1-dimensional and higher-dimensional concepts, where the instances of a k-dimensional concept are k-tuples of vertices of a graph. The tractability results we obtain for the 1-dimensional case are stronger and more general, and they are much easier to prove. In particular, our learning algorithm in the higher-dimensional case is only fixed-parameter tractable in the size of the graph, but not in the size of the training sequence, and we give a hardness result showing that this is optimal. By comparison, in the 1-dimensional case, we obtain an algorithm that is fixed-parameter tractable in both.